Mathématiques pour un anniversaire
(André Brouty octobre 2006)(André Brouty)
Cet exposé est sous licence libre LLDD.
Une question surprenante
Il arrive parfois que l'on pose à quelqu'un dont on sait qu'il connait un peu les mathématiques des questions surprenantes et pour le moins inattendues auxquelles il n'aurait pas pensées. C'est ainsi qu'un jour, une amie, pour fêter les 50 ans d'un de ses collègues, me demanda une formule mathématique la plus compliquée possible qui vale 50 ! Etonnant comme question! D'abord qu'est-ce qu'une formule compliquée ? On peut compliquer à l'infini une formule, il n'y a pas de formule la plus compliquée possible. Je compris qu'elle voulait une formule esthétique et suffisamment compliquée pour surprendre ou étonner. Mais qu'est-ce que l'esthétisme en mathématique ? Je me mis à y réfléchir et finalement je lui proposais les trois formules suivantes:
 (formule 1)
(formule 1)
 (formule 2)
(formule 2)
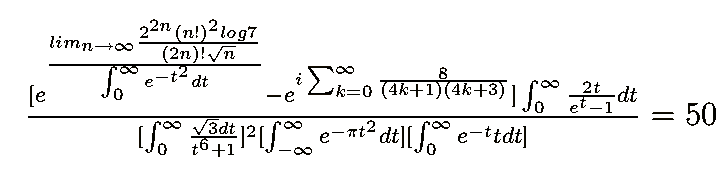 (formule 3)
(formule 3)
que je trouve assez complexes et difficiles à comprendre au premier coup d'oeil et d'un esthétisme agréable. On y trouve rassemblés les principaux symboles des mathématiques supérieures.
Comment fabriquer ces formules ?
Fabriquer ces formules à partir du nombre 50 est, somme-toute, assez simple. Il suffit de décomposer 50 de manière astucieuse et de remplacer les composantes par des formules classiques dont on connait les valeurs. Commençons par écrire:50 = 49 + 1 soit 50 = 72 + 1(4)
jusque la tout le monde comprend. Mais allons plus loin et continuons la décomposition:
72 + 1 = e2 log(7) + 1(5)
voila qu'apparaissent les logarithmes et les exponentielles, on est sur la bonne voie, continuons et occupons-nous du 2 devant log(7):
2 = √π/(√π/2)(6)
on fait maintenant apparaître le nombre pi (π) dont on sait qu'il est limite de nombreuses séries et intégrales, ce qui va nous amener petit à petit aux formules présentées ci-avant. Le nombre π1/2 peut s'écrire de multiples façons:
√π = limn->∞ 22n(n!)2/(2n)!√nformule de Wallis (7)
√π/2 = ∫0+∞e-t2dtintégrale de Gauss (8)
La formule (7) sur la formule (8) vaut le 2 de la formule (6) et donc la partie gauche de la formule (1) vaut 72.
Occupons nous maintenant du 1 de la formule (4) ce qui donnera la partie droite de la formule (1)
1 = -eiπformule d'Euler (9)
π = Σk=0k=∞8/(4k + 1)(4k + 3)formule de Leibniz (10)
La combinaison des formules (9) et (10) donne la partie droite de la formule (1) qui est ainsi complètement expliquée.
La formule (2) est obtenue à partir de la formule (1) en multipliant et en divisant par le nombre π représenté de différentes façons:
π = ∫0+∞3dt/(t6 + 1)intégrale d'une fraction rationnelle (11)
1 = ∫-∞+∞e-πt2dtintégrale de Gauss (12)
changement de variable t -> πt
La formule (3) est obtenue à partir de la formule (1) en multipliant et divisant par le nombre π2/3:
π2/3 = ∫0+∞2tdt/(et - 1)intégrale eulérienne (13)
1 = ∫0+∞te-tdtintégrale eulérienne (14)
D'où viennent ces formules ?
On trouvera comment établir ces formules très classiques dans la bibliographie suivante:
- Le petit Archimède, Numéro spécial sur pi (mai 1980)
- Jean-Paul Delahaye, Le fascinant nombre pi (Belin 1997)
- Pierre Eymard, Jean-Pierre Lafon, Autour du nombre pi (Hermann 2000)
Présentation artistique des formules
Il est possible de travailler ces formules avec un logiciel de traitement d'images. Pour ma part j'ai entré la formule (3) dans le traitement de texte OpenOffice avec des polices antialiasing, puis j'en ai fait des saisies d'écran que j'ai travaillées ensuite dans le logiciel Gimp pour en obtenir l'image suivante. Si d'autres artistes veulent faire d'autres modèles je veux bien les héberger dans une galerie en citant leurs auteurs. A vos pinceaux Gimp!